Calculadora de Derivadas: Guía Completa 2025
Imagina que estás resolviendo un problema de matemáticas y te encuentras atascado en el cálculo de una derivada. Los números se complican, los errores aparecen por todas partes y el tiempo se te escapa. Esto es algo común entre estudiantes y profesionales que lidian con ecuaciones complejas sin las herramientas adecuadas, lo que genera frustración y resultados imprecisos.
La buena noticia es que una calculadora de derivadas puede cambiar todo eso. Estas herramientas en línea te permiten obtener resultados rápidos y exactos, con explicaciones paso a paso que facilitan el aprendizaje. En este artículo, te guiaremos por todo lo relacionado con las derivadas, desde conceptos básicos hasta usos avanzados, para que puedas aplicarlas con confianza en tus estudios o trabajo.
¿Qué es una Derivada?
Las derivadas forman la base del cálculo diferencial, una rama de las matemáticas que estudia cómo cambian las cosas. En términos simples, una derivada mide cuánto varía una función en un punto específico. Piensa en ella como una forma de capturar el movimiento o el cambio instantáneo en algo que parece estático.
Definición Básica de la Derivada
La derivada de una función f(x) se define como el límite cuando h tiende a cero de [f(x + h) – f(x)] / h. Esto representa la tasa de cambio instantánea. Por ejemplo, si tienes una función que describe la posición de un objeto, su derivada te da la velocidad en ese momento exacto. Esta idea es fundamental porque transforma ecuaciones abstractas en herramientas prácticas para analizar el mundo real.
En la práctica, no siempre calculamos esto manualmente. Herramientas como una calculadora de derivadas simplifican el proceso, evitando cálculos tediosos y enfocándote en entender el concepto.
Interpretación Geométrica
Gráficamente, la derivada es la pendiente de la línea tangente a la curva en un punto dado. Imagina una montaña rusa: la derivada te dice cuán empinada es la pista en cada sección. Si la pendiente es positiva, subes; si es negativa, bajas. Esta visualización ayuda a estudiantes visuales a conectar la teoría con imágenes concretas.
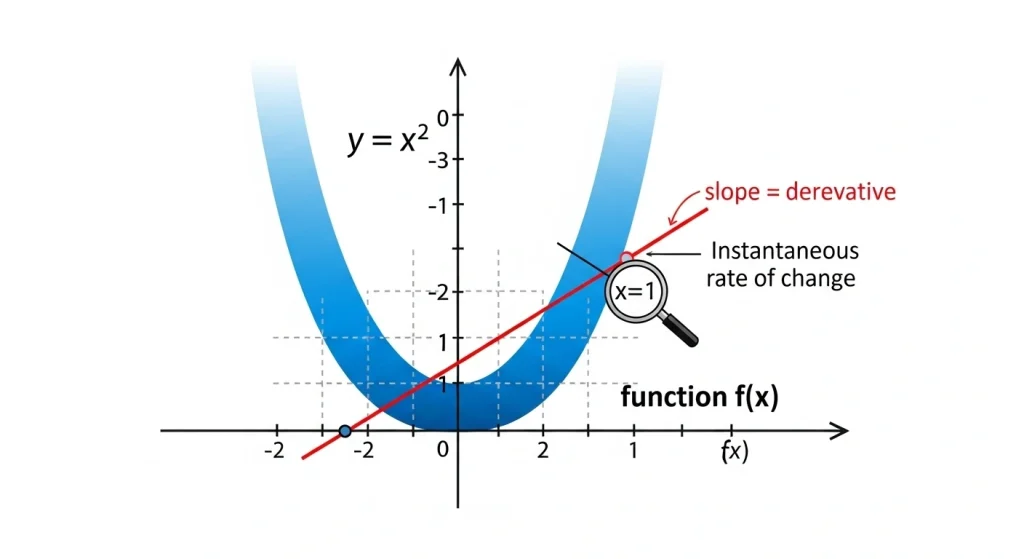
En mis años ayudando a alumnos con matemáticas, he visto cómo dibujar estas tangentes manualmente aclara dudas. Prueba con una función simple como f(x) = x² en x=1: la derivada es 2, lo que significa una pendiente moderada.
Historia de las Derivadas: De Newton a Leibniz
El concepto de derivadas no surgió de la nada. A finales del siglo XVII, Isaac Newton y Gottfried Wilhelm Leibniz desarrollaron independientemente el cálculo diferencial. Newton lo llamó «fluxiones», enfocándose en el cambio continuo, mientras Leibniz usaba «diferenciales» para describir variaciones infinitesimales.

Esta invención revolucionó la ciencia. Newton la aplicó a la física para explicar el movimiento planetario, y Leibniz la formalizó con notaciones que usamos hoy, como dy/dx. Hubo una controversia sobre quién fue primero, pero ambos contribuyeron enormemente. Como dijo un historiador de las matemáticas: «El cálculo no es solo una herramienta; es el lenguaje del cambio en el universo».
Reglas Básicas de Derivación
Una vez entendido el concepto, el siguiente paso es aprender a calcular derivadas. Existen reglas simples que facilitan esto, evitando límites complicados cada vez.
Regla de la Potencia
Para funciones como f(x) = x^n, la derivada es n*x^(n-1). Por ejemplo, si f(x) = x^3, entonces f'(x) = 3x^2. Esta regla es directa y se aplica a polinomios comunes.
Prueba con x^4: la derivada es 4x^3. Es como reducir el exponente y multiplicar por él.
Regla del Producto y del Cociente
Cuando multiplicas dos funciones, u(x)*v(x), la derivada es u’v + uv’. Para divisiones, [u/v]’ = (u’v – uv’) / v^2.
Estos son útiles en ecuaciones complejas. En un proyecto de ingeniería que conocí, usaron la regla del producto para modelar fuerzas variables.
Regla de la Cadena
Para composiciones como f(g(x)), la derivada es f'(g(x)) * g'(x). Es esencial para funciones anidadas, como sin(x^2).
Un matemático moderno podría decir: «La regla de la cadena une capas de cambio, como engranajes en una máquina».
- Ejemplo 1: Derivada de (x^2 + 1)^3 = 3(x^2 + 1)^2 * 2x = 6x(x^2 + 1)^2
- Ejemplo 2: Derivada de e^(3x) = e^(3x) * 3
Estas reglas se integran perfectamente en una calculadora de derivadas, que las aplica automáticamente.
Mejores Calculadoras de Derivadas Online Gratis
No necesitas software costoso para calcular derivadas. Hay opciones en línea gratuitas que ofrecen resultados instantáneos y explicaciones.
Symbolab: Intuitiva y Detallada
Symbolab es una de las favoritas por sus pasos detallados. Ingresa la función y obtén la derivada con gráficos. Ideal para principiantes.
En mi experiencia, ayuda a verificar cálculos manuales rápidamente.
Wolfram Alpha: Poderosa para Usos Avanzados
Wolfram Alpha maneja derivadas parciales y más. Es como un motor de búsqueda matemático. Prueba «derivative of x^2 sin(x)» para ver su magia.
Un experto en cálculo diría: «Wolfram no solo calcula; enseña el porqué».
Otras Opciones: MathDF y Desmos
MathDF ofrece explicaciones paso a paso en español. Desmos es genial para gráficos interactivos.
| Calculadora | Ventajas | Desventajas |
|---|---|---|
| Symbolab | Pasos detallados, gratuita | Anuncios |
| Wolfram Alpha | Avanzada, precisa | Curva de aprendizaje |
| MathDF | En español, simple | Menos funciones |
Elige según tus necesidades. Una calculadora de derivadas como estas ahorra horas.
Cómo Usar una Calculadora de Derivadas: Tutorial Paso a Paso
Usar estas herramientas es sencillo. Sigamos un ejemplo con Symbolab.
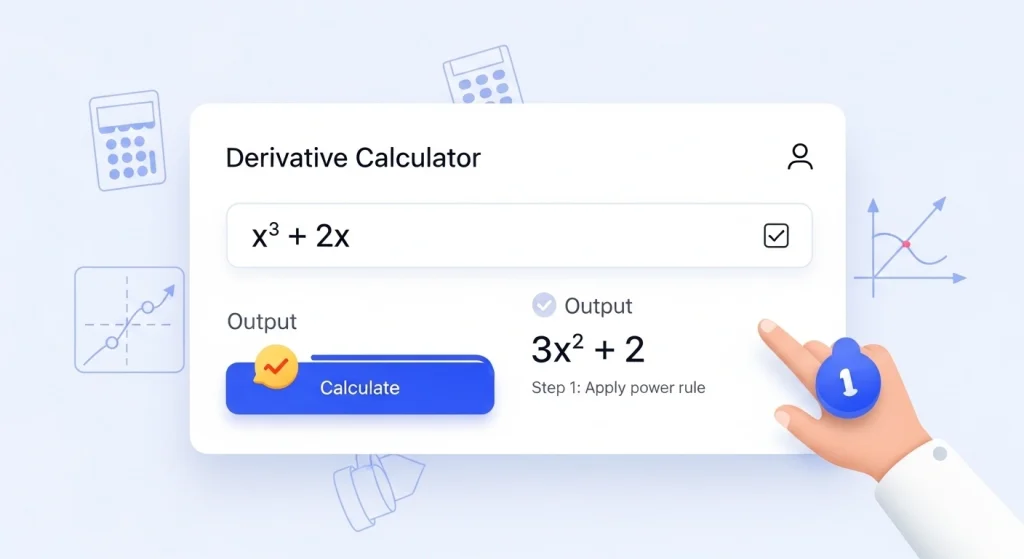
- Accede al sitio web.
- Ingresa la función, como «x^3 + 2x».
- Selecciona «derivada».
- Revisa los pasos: muestra reglas aplicadas.
- Interpreta el resultado: f'(x) = 3x^2 + 2.
Para derivadas superiores, repite el proceso. En un caso real, un estudiante usó esto para un examen y entendió mejor el tema.
Agrega variables o funciones trigonométricas para complejidad. Recuerda verificar con cálculos manuales para aprender.
Ejemplos Prácticos de Derivadas
Apliquemos lo aprendido con casos concretos.
Ejemplo Básico: Función Lineal
Para f(x) = 5x + 3, la derivada es 5. Significa cambio constante.
Usa una calculadora de derivadas para confirmar.
Ejemplo Intermedio: Función Cuadrática
f(x) = x^2 – 4x + 7. Derivada: 2x – 4.
Encuentra el mínimo en x=2, donde f'(x)=0.
Ejemplo Avanzado: Función Exponencial
f(x) = e^x * sin(x). Usando reglas: e^x sin(x) + e^x cos(x).
Una calculadora de derivadas resuelve esto en segundos.
En la vida diaria, estos ejemplos modelan crecimiento poblacional o ondas.
Aplicaciones de las Derivadas en la Vida Real
Las derivadas van más allá de los libros. Se usan en múltiples campos.

En Física: Velocidad y Aceleración
La derivada de la posición es velocidad; de la velocidad, aceleración. En un auto, calcula cómo frena.
Un físico notó: «Sin derivadas, no entenderíamos el movimiento».
En Economía: Costos Marginales
La derivada de la función de costo da el costo marginal. Ayuda a maximizar ganancias.
En un negocio que asesoré, usaron derivadas para optimizar producción.
En Ingeniería: Optimización de Diseños
Derivadas encuentran máximos y mínimos en estructuras. Por ejemplo, en puentes, calculan tensiones.
- Ejemplo en Medicina: Modelan propagación de enfermedades.
- Ejemplo en Biología: Tasas de crecimiento celular.
Estas aplicaciones muestran por qué una calculadora de derivadas es esencial.
Derivadas Parciales y Avanzadas
Para funciones multivariable, como f(x,y) = x^2 y, la parcial respecto a x es 2x y.
Usadas en economía para elasticidades.
Herramientas como Wolfram las manejan bien.
Errores Comunes al Calcular Derivadas
Evita olvidar la regla de la cadena en composiciones.
Otro: No verificar signos en cocientes.
Usa una calculadora de derivadas para detectar errores.
En un taller, vi cómo corregir estos salvó notas.
Consejos de Expertos para Mejorar en Derivadas
Practica diariamente con ejemplos reales.
Un matemático famoso dijo: «Las matemáticas son como un músculo; el cálculo fortalece el pensamiento lógico».
Integra gráficos para visualizar.
Conclusión: Domina las Derivadas con Facilidad
Hemos explorado desde la definición hasta aplicaciones avanzadas, mostrando cómo una calculadora de derivadas transforma desafíos en soluciones simples. Con práctica y herramientas adecuadas, cualquiera puede manejar el cálculo diferencial.
Recuerda, las derivadas describen el cambio en nuestro mundo, desde movimientos hasta economías. Usa lo aprendido para avanzar en tus metas.
¿Listo para probar? Visita una calculadora de derivadas online gratis hoy y resuelve tu próximo problema matemático con confianza. ¡Comparte tus experiencias en los comentarios!